Binary Search Tree

• An ordered binary tree
• For every node, all elements in its left subtree are less and any elements in its right subtree are greater
• Used because they can quickly search and sort
• Height (N is number of nodes)
  • Average: $O(\log N)$
  • Worst case: $N-1$

Terminology

• Predecessor: Left subtree’s rightmost node
• Successor: Right subtree’s leftmost node-

Operations

Operation	Best Case	Worst Case
Searching	$O(\log n)$	$O(n)$
Insertion	$O(\log n)$	$O(n)$
Deletion	$O(\log n)$	$O(n)$

Searching

search(target, root)
	if the tree is empty
		return null
	else if target == root.data
		return root.data
	else if target < root.data
		return seach(root.left)
	else
		return search(root.right)

Time complexity:

• Worst case: $O(n)$ (when tree is basically a linked list)
• Average case: $O(\log n)$

Insertion

TreeNode insert(item, root)
	if root == null
		return TreeNode(item)
	else if item < root.data
		root.left = insert(item, root.left)
	else
		root.right = insert(item, root.right)
	return root

Deletion

delete(item, root)
	if root == null
		// item is not in tree
		return null
	if item < root.data
		root.left = delete(item, root.left)
	else if item > root.data
		root.right = delete(item, root.right)
	else //the item is in the local root
		if root has no children
			delete root
			return null
		else if root has one child
			child = root.child // the one that exists
			delete root
			return child
		else // replace with inorder successor
			successor = getMinimum(curr->right);
			val = successor.val
			delete(val, root) // delete successor
			root.val = val
	return root

Traversal

• Iterating over a tree such that you touch every node
• Two strategies
  • Depth First: Goes down an entire branch
  • Breadth First: Goes through and entire level

Depth First

traverse(root)
	if root == null
		return
	else
		// order changes depending on type of traveral
		traverse(root.left)  // L
		visit root           // N
		traverse(root.right) // R

• Uses a stack (through recursion typically)
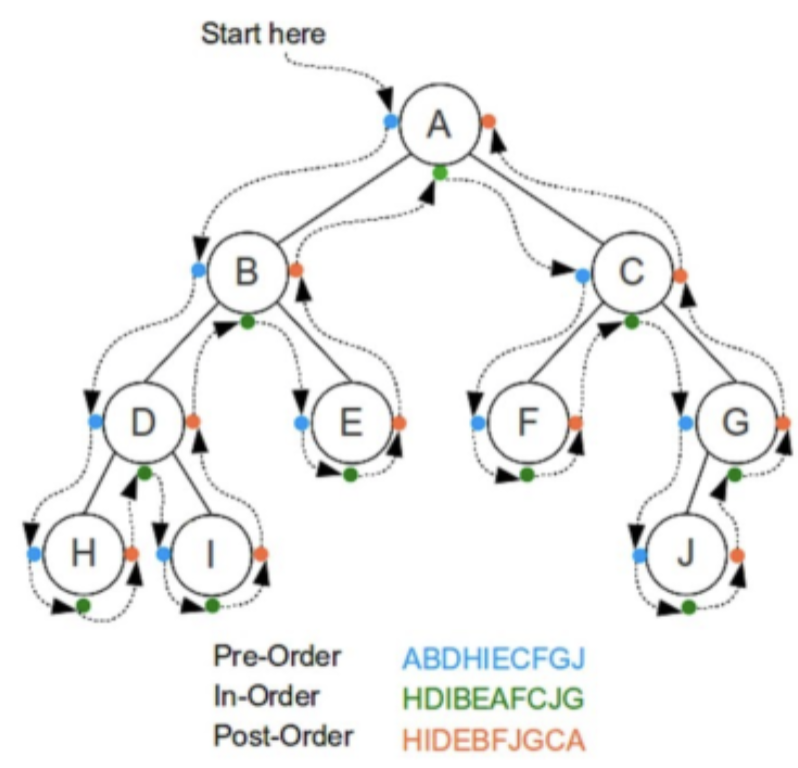
• Inorder
  • Order: LNR
  • Uses
    • Returns the sequence in ascending order
    • Is able to get a sorted list in O(n)
• Preorder
  • Order: NLR
  • Work at a node is done before (pre) its children
  • Uses
    • Printing dictionary listing
    • Making a copy of a tree
  • The true depth first search (goes down an entire branch at a time)
• Postorder
  • Order: LRN
  • Work at a node is done after (post) its children
  • Uses
    • Deallocating every node in a tree
    • Calculating an accumulated sum for each node and all descendants
• Strategy for quickly reading
  • 

Breadth First

• AKA Level Order
• Types
  • Spiral approach (always L→R or R→L)
  • Zig Zag approach (alternates direction for each line)
• Uses a queue
  • “Queue… I’m out of breadth”

void levelOrder(TreeNode* root) {
	queue<TreeNode*> q;
 
	if(root != nullptr) {
	    q.push(root);
	}
 
	while (!q.empty()) {
		cout << q.front();
		
		if (q.front()->left != nullptr)
			q.push(q.front()->left);
 
		if (q.front()->right != nullptr) 
			q.push(q.front()->right);
 
		q.pop();
	}
}