Planes
Planes
Definitions
Geometric
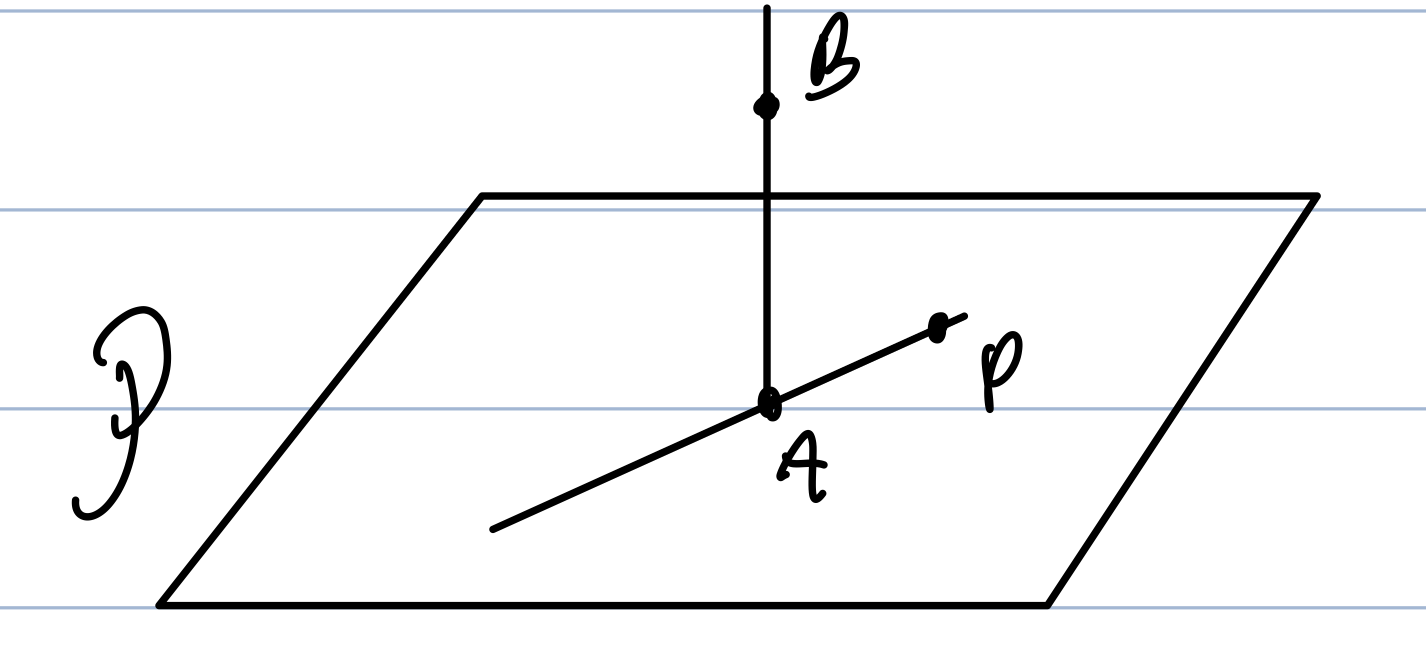
P={P∣AB⊥AP}
Algebraic
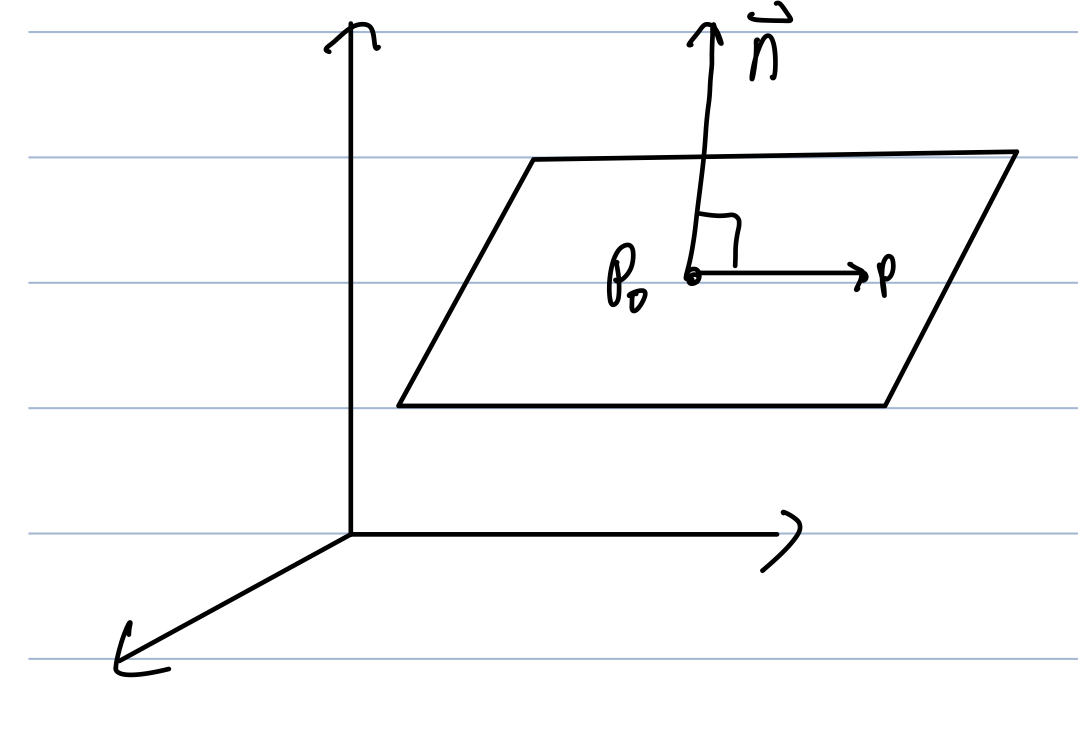
- Values
- Point on plane: P0=(x0,y0,z0)
- Normal vector: n=⟨n1,n2,n3⟩
- Equation
- n1(x−x0)+n2(y−y0)+n3(z−z0)=0
- n1x+n2y+n3z=n⋅OP=d
- Important Bits
- P∈P⟺n⊥P0P⟺n⋅P0P=0
- Equation: n1x+n2y+n2z=d
Properties
- Normal vector: n⊥P
- Can be used to find if other vectors are parallel/perpendicular
- Can be used to find the angle between planes
- A particular point: P0∈P
Coordinate Planes
- Planes that are only offset in a single axis
- In the form x/y/z=c
Parallel Planes
- Planes are parallel if their normal vectors are the same
- so only the d value is different in the algebraic definition
- Distance between parallel planes
D=∥n∥∣d1−d2∣
Points to Plane
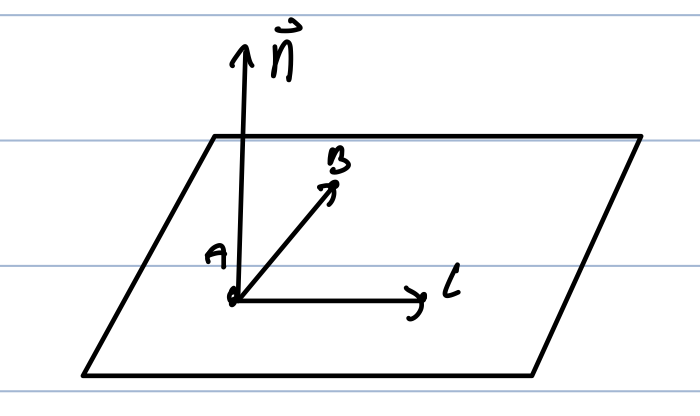
n=AB×ACP0=A
Distance From a Point to a Plane
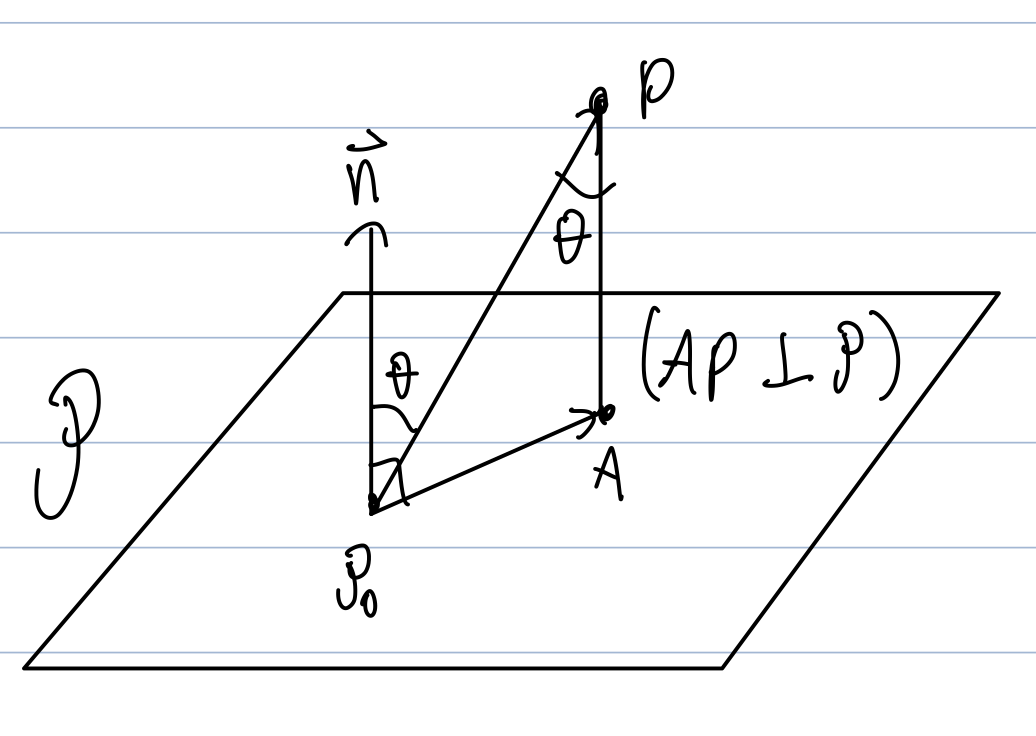
D=∥n∥P0P⋅n


