Arithmetic Operations

Integers

Addition

• Just do it like decimal addition with add and carry
• Overflow if the result is out of range
  • Pos + Neg: No Overflow possible
  • Pos + Pos: Overflow if sign bit is 1
  • Neg + Neg: Overflow if sign bit is 0
  • (you know it overflowed if the sign bit flipped)

Subtraction

• Don’t actually subtract, add a positive to a Two’s Complement
• Overflow if
  • Pos - Pos, Neg - Neg: No overflow possible
    • Same as Pos + Neg
  • Neg - Pos: Overflow if sign bit is 0
    • Same as Neg + Neg
  • Pos - Neg: Overflow is sign bit is 1
    • Name as Pos + Pos

Multiplication

• Start with long-multiplication approach
• Length of product is the sum of operand lengths
• Don’t use two’s complements numbers, just use multiplication rules for sign and add it back at the end
• Hardware
  • Unoptimized
    • 
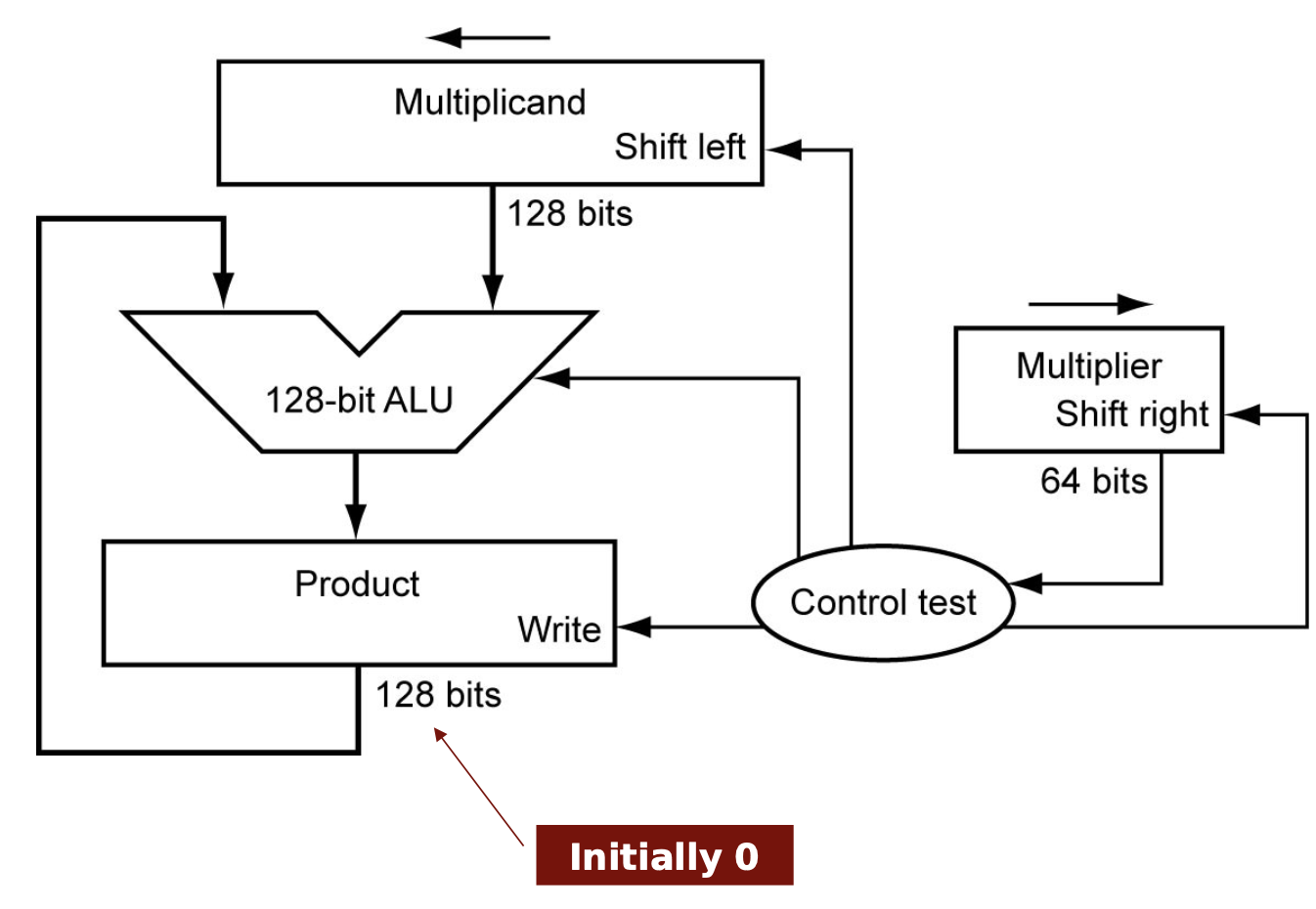
    • For each digit in the multiplier
      • Logical shift the multiplicand left
      • If the digit in the multiplier is 1, add that number to the intermediate product
  • Optimized
    • 
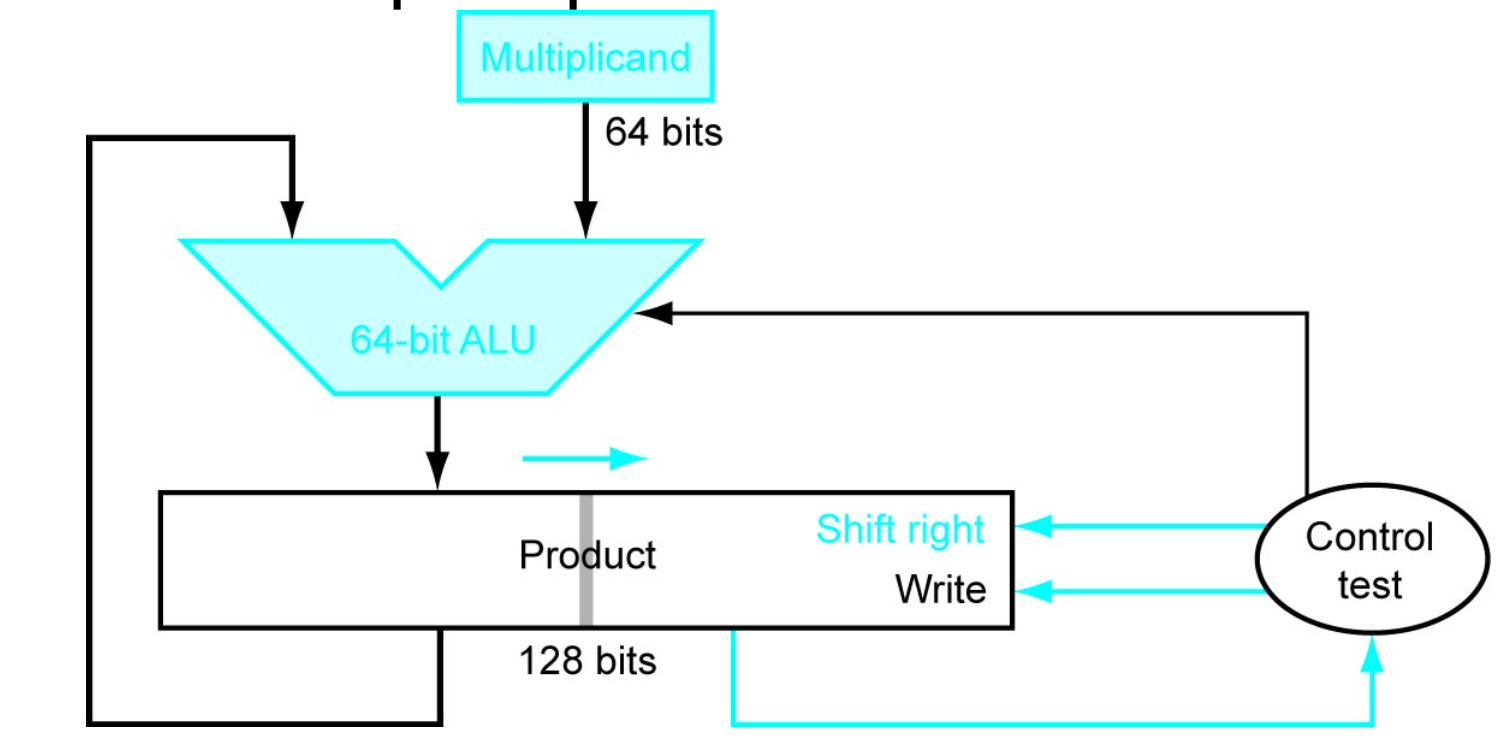
    • Multiplier is initially placed in the right half of the product register
    • need to go over the steps how this works
  • Faster Multiplier
    • Uses multiple adders
      • Calculates every step of the multiplication at once
      • Cost/performance tradeoff
    • Can be pipelined
      • Several multiplication performed in parallel
    • 
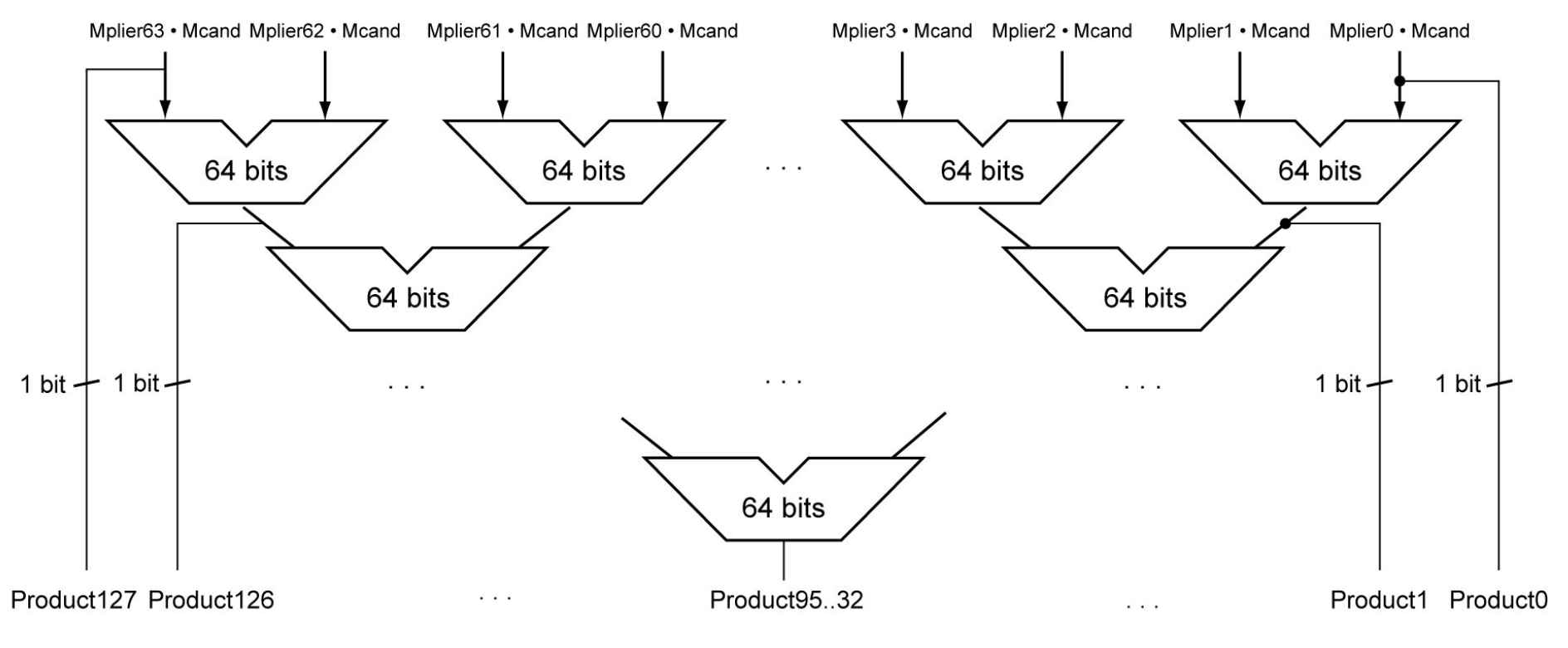
    • ${\log }_{2}n$ levels of adders
      • $n$ cycles → ${\log }_{2}n$ cycles
• Instructions
  • MUL: Multiply
    • Gives the lower 64 bits of the product
    • What we can just use in class (assume no inputs will overflow)
  • SMULH: Signed multiply high
    • Gives the upper 64 bits of the product, assuming the operands are signed
  • UMULH: Unsigned multiply high
    • Gives the upper 64 bits of the product, assuming the operands are unsigned

Division

• Use long division
• Steps
  • Check for 0 divisor
  • Long division approach
    • If divisor ⇐ dividend bits
      • 1 bit in quotient, subtract
    • Else
      • 0 bit in quotient, bring down next dividend bit
  • Restoring division
    • Do the subtract, and if remainder goes < 0, add divisor back
  • Signed division
    • Divide using absolute values
    • Add sign bit back at the end
• n-bit operands yield n-bit quotient and remainder
• Instructions
  • SDIV X1, X2, X3 → X1 = X2 / X3 (signed)
    • X1 contains the quotient (remainder is lost)
    • If you need the remainder perform
      • SDIV X1, X2, X3 // X1 has quotient
      • MSUB X4, X2, X3, X2 // X4 = X2 – X1 * X3
      • MSUB works because remainder = dividend - quotient * divisor
  • UDIV (unsigned)
• Hardware
  • Very similar to the multiplication
  • Cannot be parallelized
    • Because you cannot do the next step until you find the intermediate remainder when doing long division

Floating Point

Addition

• Steps
  1. Align binary points
     • Shift number with smaller exponent
  2. Add significands (the fractional component)
  3. Normalize result and check for over/underflow
  4. Round and renormalize if necessary
• Hardware
  • Much more complex than integer adder
  • Usually takes several clock cycles (but can be pipelined)
• For signs, just do it in your head because how it is actually handled is out of scope
• Because of rounding, associativity sometimes does not apply to floating point operations

Multiplication

• Steps
  1. Add exponents
     • For biased exponents, subtract bias from sum
  2. Multiply significands
  3. Normalize results and check for over/underflow
  4. Round and renormalize if necessary
  5. Determine sign of result form signs of operands
• Hardware
  • Lot of similar complexity to FP adder
    • But uses a multiplier for significands instead of an adder

Hardware

• FP arithmetic hardware usually does
  • Addition (4), subtraction (4), multiplication (7), division (~20), reciprocal (~20), square-root (a lot)
    • Numbers are the time in unit of the time that integer addition takes
  • FP ←> integer conversion
• Operations take several cycles but can be pipelined

Instructions

• Seperate FP registers
  • 32 single precision: S0, …, S31
  • 32 douple-precision: DS0, …, DS31
  • Sn stored in the lower 32 bits of a Dn
• FP instructions operate only on FP registers
• Load/Store
  • Single precision: LDURS, STURS
  • Double precision: LDURD, STURD
• Single-precision arithmetic
  • FADDS, FSUBS, FMULS, FDIVS
• Double-precision arithmetic
  • FADDD, FSUBD, FMULD, FDIVD
• Single- and double-precision comparison
  • FCMPS, FCMPD

Multimedia

• Graphics and media processing operates on vectors of 8-bit and 16-bit data types
• SIMD = Single instruction, multiple data
• Multiple values can be stored in one register
• When doing arithmetic, carry is disabled on the border between the sections