Divider
- Division (x = qy + r) after “restoring algorithm”
Classic Method
- Assuming always yi=1 then subtract the divisor
- If the result is positive, then move to the next digit
- If the result is negative, then set yi=0 and add the divisor back (i.e. cancel the subtraction)
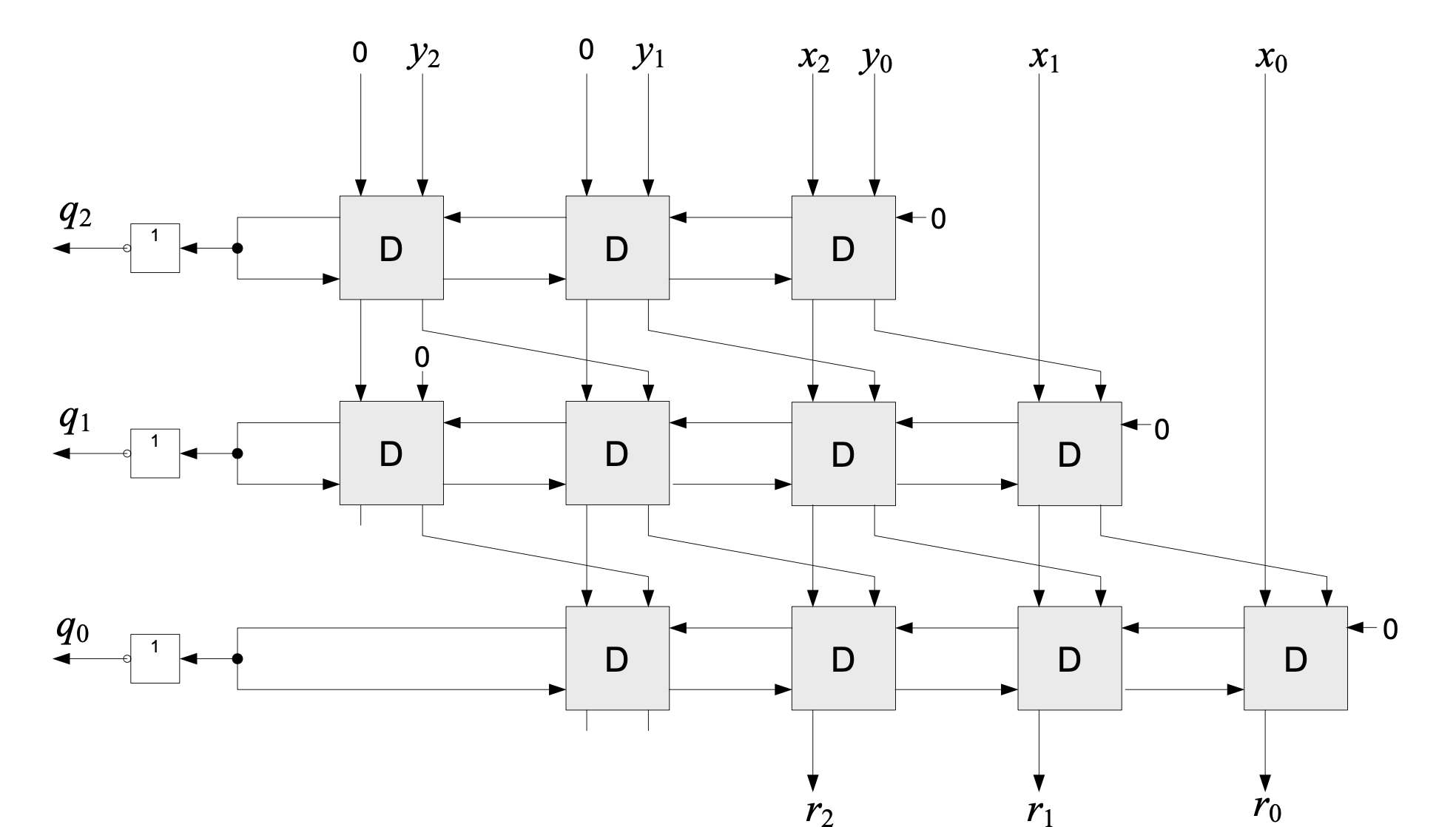
Array Divider
- Performs the division as a combinational circuit
- 1 subtractor (ex: ripple-borrow subtractor) is needed per row
- How to perform correction in case of negative result?
- The result is negative when the borrow (left most bit) is equal to ‘1’
- Feed the borrow back (right) as signal a
- a=0 the subtraction was correct, no need to correct
- a=1 instead of the difference, use the minuend
- Special full subtractor the “D-Box”
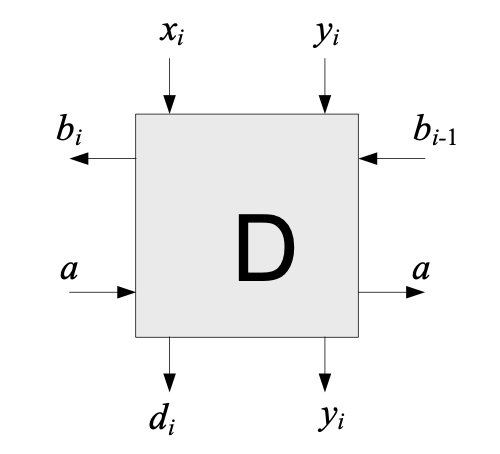
- di=axi+a(xi⊕yi⊕bi−1)
- bi=xiyi+xibi−1+yibi−1
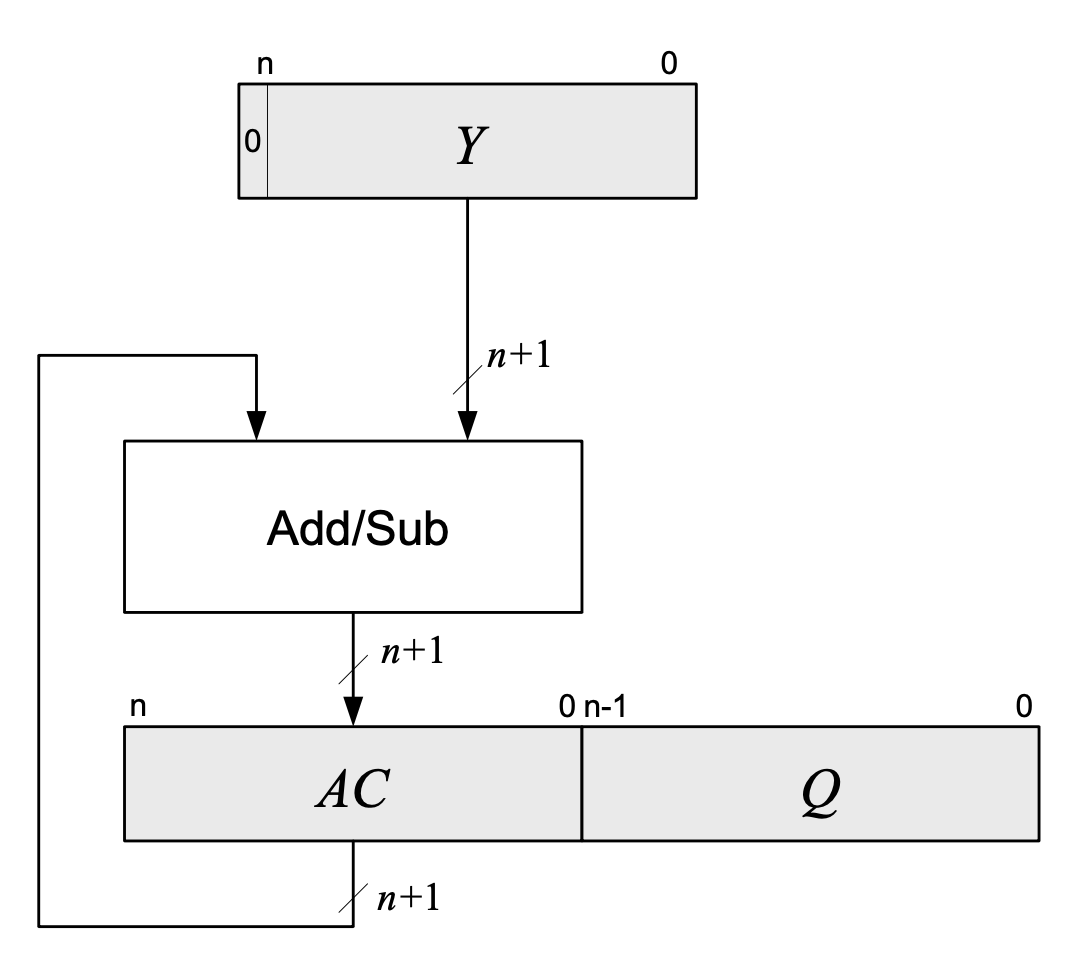
Sequential Divider
- Quotient is computed stepwise
- Algorithm
- Load operand into register Y
- AC ← 0, Q ← X
- Iterate n times
- shift (AC, Q) one position left
- AC ← AC - Y
- If AC < 0
- then AC ← AC + Y
- else Q(0) ← 1
- Quotient is in Q, remainder is in AC
- Notes
- Uses logic shift (fill left with 0)
- AC and Y are (n+1) bit numbers in 2’s complement