Binary Real Numbers

Fractions

• Fraction is not a whole number (stuff past the decimal point)
• Represents how many negative powers fit in
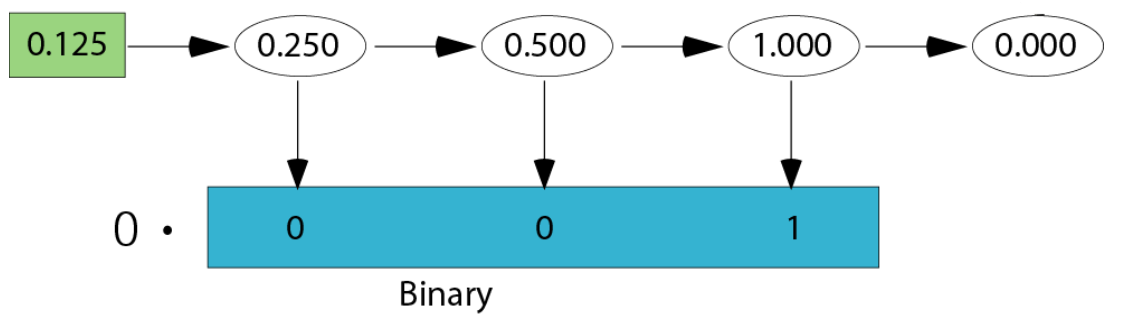
• Fractional Decimal → Binary
  1. Write the fraction in the left corner
  2. Multiply the number by 2 and extract the integer part as the binary (written below)
  3. Repeat, moving to the right, until the number is 0.0
• 

Fixed Point

• N bits available, divided into the integer and fraction components
• Conversion: Convert integer and fraction parts separately

Floating Point

• Base 2 scientific notation
• Normalized Representation
  • The form $\pm 2^{\text{exp}}\cdot 1.\text{xx}\dots$
  • 1.xx is a binary fraction that always starts with 1 (to save space)
• Stored as
  • Sign
    • 0 positive, 1 negative
  • Exponent
    • Stored using a Bias
  • Mantissa
    • Numbers after decimal point
    • Filled with 0s to the right (because it’s a fraction)
• Sizes
  • Single Precision (32 bits)
    • Sign: 1
    • Exp: 8 (excess 127)
    • Mantissa: 23
  • Double Precision (64 bits)
    • Sign: 1
    • Exp: 11 (excess 1023)
    • Mantissa: 52
• Decimal → FP Steps
  1. Convert integer and fractional components to binary
  2. Normalize
  3. Convert exponent to excess representation
  4. Assemble into final representation
• Range
  • With a $k$ bit mantissa
  • $[-(2-2^k)\cdot e^{E_{max}},+(2-2^{-k})\cdot 2^{E_{max}}]$

Operations

• Addition/Subtractions
  1. Identify the operand with the bigger exponent
  2. Shift the mantissa of the operand with smaller exponent to the left until the two exponents match
  3. Perform the addition/subtraction of the resulting mantissa
  4. Normalize the result
  5. Perform underflow/overflow test
• Multiplication
  1. Sign = product of signs
  2. Add exponents
  3. Multiply mantissa
  4. Normalize if needed
  5. Underflow/overflow test

Special Cases

Exponent	Fraction	Represents
0	0	0
0	Nonzero	+- denormalized
1-254	Anything	+- floating point
255	0	+- infinity
255	Nonzero	Nan