Finite State Automata

• Has inner states, reads input signals, and writes output signals
• Uses Combinational Logic and Sequential Logic to model multiple possible states

Mealy Automata

• A tuple $A=(X,Y,S,\delta ,\lambda ,s_1)$
  • $X$: Finite, non-empty set of input symbols
  • $Y$: Finite, non-empty set of output symbols
  • $S$: Finite, non-empty set of states
  • $\delta :S\times X\to S$ (state transition function)
  • $\lambda :S\times X\to Y$ (output function)
  • $s_1$: Initial state
• Outputs are linked to the edges

State Transition Table

• Table in which the rows represent states and columns represent input symbols
• An entry $(\delta (s,x)/\lambda (s,x))$ captures the transition from state $s\in S$ with the input symbol $x\in X$ to state $\delta (s,x)$ with output $\lambda (s,x)$

State Transition Graph

• A state transition graph is a directed graph in which nodes represent states and edges represent transitions
  • Edges are labeled with the values of the transition function
  • The node without precedence is the initial state

Categories

• Deterministic if: $\forall x\in X,\forall s\in S:|\delta (s,x)|\le 1$
  • Not more than one option for a given input at each given state
• Complete if: $\forall x\in X,\forall s\in S:|\delta (s,x)|\ge 1$
• Both: $\forall x\in X,\forall s\in S:|\delta (s,x)|=1$
• We limit ourselves in this class to deterministic and complete
  • Non-complete automata model incomplete specifications
  • Non-deterministic automata are used in analysis and verification of sequential circuits

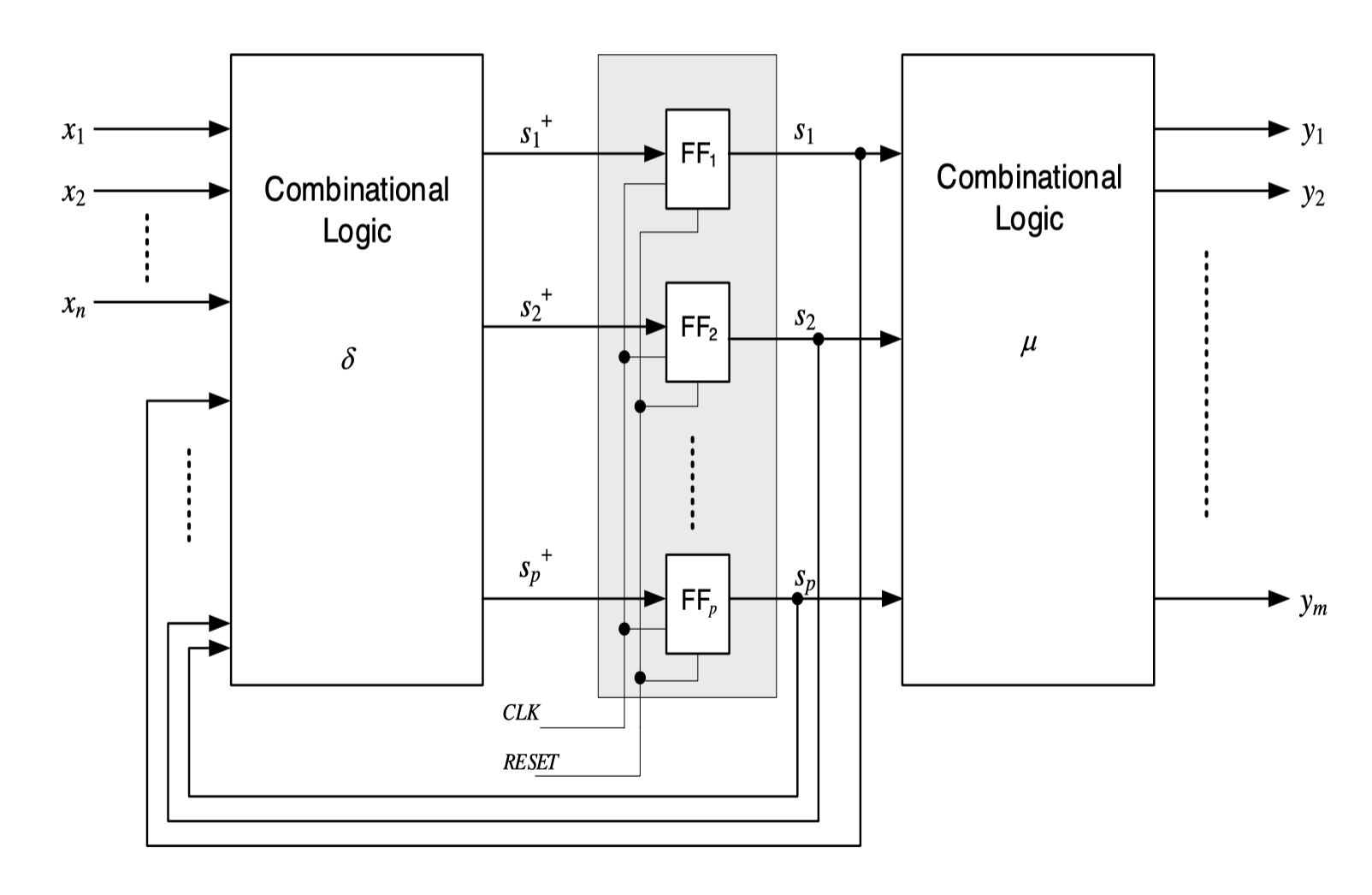
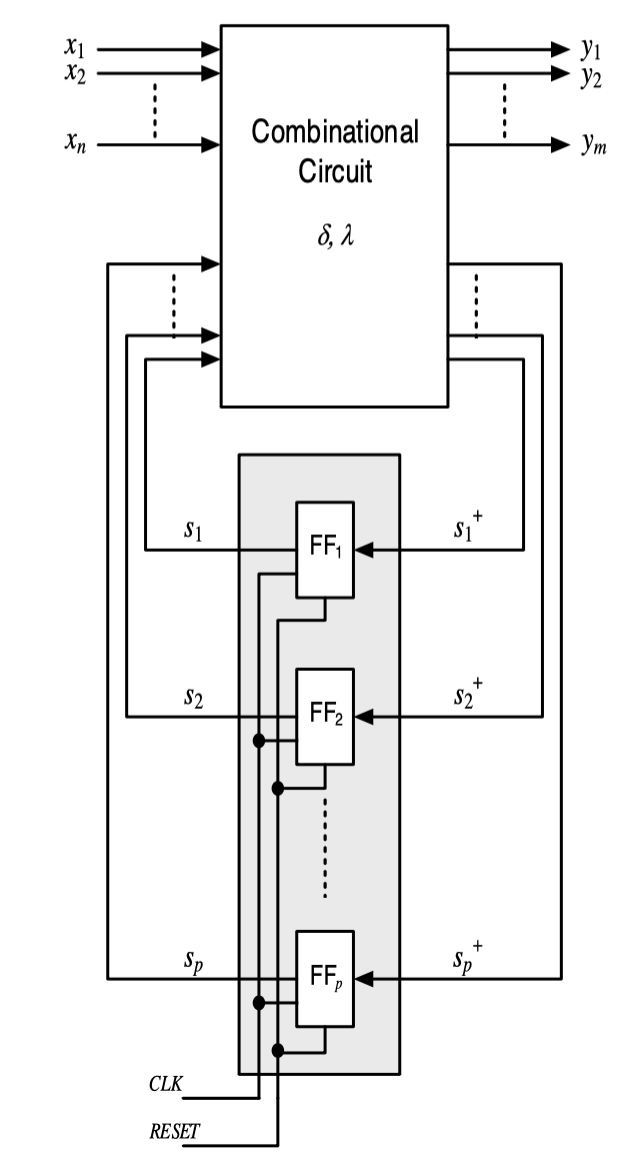
Hardware Implementation

• Finite state machines = technical realization of automata
• Structured using huffman normal form
• Symbols X, Y, and S are binary coded
• 

Moore Automata

• A tuple $A=(X,Y,S,\delta ,\mu ,s_1)$
  • $X$: Finite, non-empty set of input symbols
  • $Y$: Finite, non-empty set of output symbols
  • $S$: Finite, non-empty set of states
  • $\delta :S\times X\to S$ (State transition function)
  • $\mu :S\to Y$ (Output function)
  • $s_1$: initial state
• The output Y depends only on the current state, not the input
  • So the input is linked to the nodes
• The output function is also known as state marking function

Hardware Implementation

• 

Design

1. Specify the automaton using state transition table/graph
   • If needed, minimize the number of states
2. Compute binary coding of the inputs and outputs. Compute the number of memory cells needed to store the states
3. Specify the combinational circuits for the functions $\delta$ and $\lambda$ or $\mu$ from the state transition table. $S^{+}=\delta (X,S)$ and $Y=\lambda (X,S)$ or $Y=\mu (S)$
4. Design of the Combinational Logic as Two Level Logic or multi-level logic

Conversion

• Moore to Mealy
  1. Mark transitions to a state with the output linked to that state
  2. Reduce
• Mealy to Moore
  1. For each state s of the mealy automaton, insert as many states as there are incident edges to s
  2. Label the new states with the output variables of the corresponding incident transitions
  3. Reduce

Comparison

• Have the same modeling power
• Moore automata need more states in general than mealy
• Output
  • Moore: change only upon state transition
  • Mealy: change with inputs
• Moore automata are more robust to short impulses of the inputs (glitches) and usually preferred to Mealy in hardware design
• Mealy-automata react faster to changes at the input