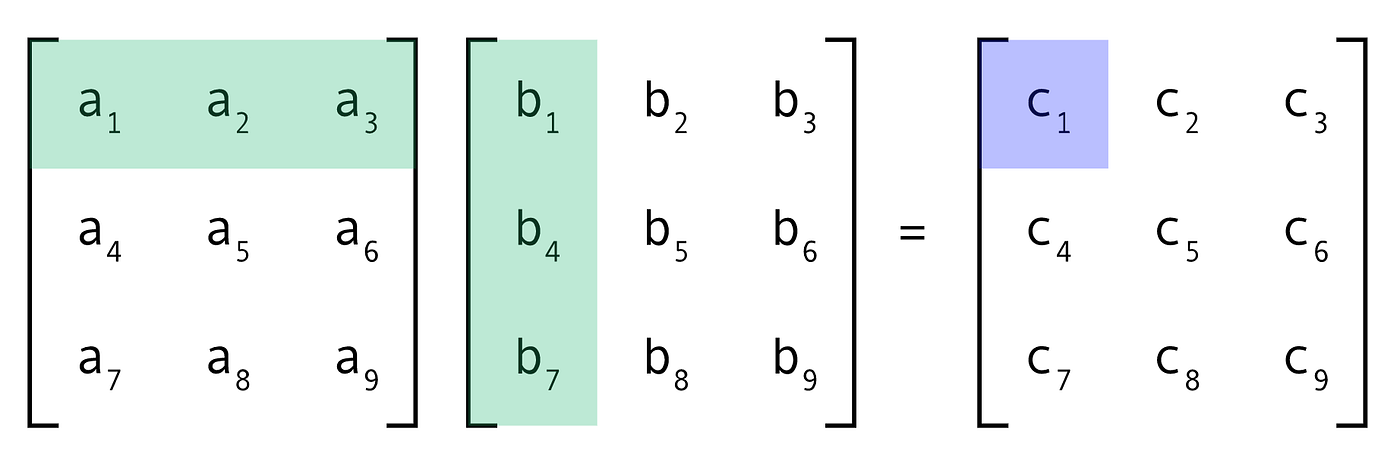
Matrix Multiplication

• Let $A_{m\times n},B_{n\times p}$
• The product $AB$ ($m\times p$) is given by the following
• $(AB{)}_{ij}={\sum }_{k=1}^n{A}_{ik}{B}_{kj}$ for $1\le i\le m$, $1\le j\le p$
  • dot product of row $i$ of $A$ with column $j$ in $B$

Properties

• For:
  • $A:m\times n$
  • $B,C:n\times p$
  • $D,E:q\times m$
• $A(B+C)=AB+AC$ and $(D+E)A=DA+EA$
• $a(AB)=(aA)B=A(aB)$
• $I_{m}A=A=A{I}_n$
• $(AB{)}^t=B^t{A}^t$
• $A(BC)=(AB)C$
• The $n\times n$ identity matrix, $I_n$, is defined by $(I_n{)}_{ij}={\delta }_{ij}$ (the kronecker delta)
  • $V$, $n$-dim vector space with ordered basis $\beta$ then $[I{]}_{\beta }=I_n$
• Theorem 2.13
  • Let $u_j$ and $v_j$ denote the $j^{th}$ column of $AB$ and $B$ respectively
  • $u_j=A{v}_j$
  • $v_j=B{e}_j$ (jth standard vector of $F^p$)

Powers

• $A^0=I_{n\times n}$
• $A^1=A$
• $A^k=A^{k-1}\cdot A$ for $k>1$

As a Linear Transform

• Left multiplication by $A$ can be represented as $L_A:F^n\to F^m$ defined by $L_a(x)=Ax$
• Properties
  • $[L_A{]}_{\beta }^{\gamma }=A$
  • $L_{A+B}=L_A+L_B$
  • $L_{aA}=a{L}_A\forall a\in F$
  • $L_{AE}=L_A{L}_E$
  • If $m=n$ then $L_{I_n}$ is the identity function $I_{F^n}$