Multipliers

Array Multiplier

• Shift and add principle
  • For $x,y\ge 0$
  • $xy=\left({\sum }_{i=0}^{n-1}{x}_i{2}^i\right)\left({\sum }_{j=0}^{n-1}{y}_j{2}^j\right)={\sum }_{i=0}^{n-1}\left(2^i\cdot \sum x_i{y}_j{2}^j\right)$
• 
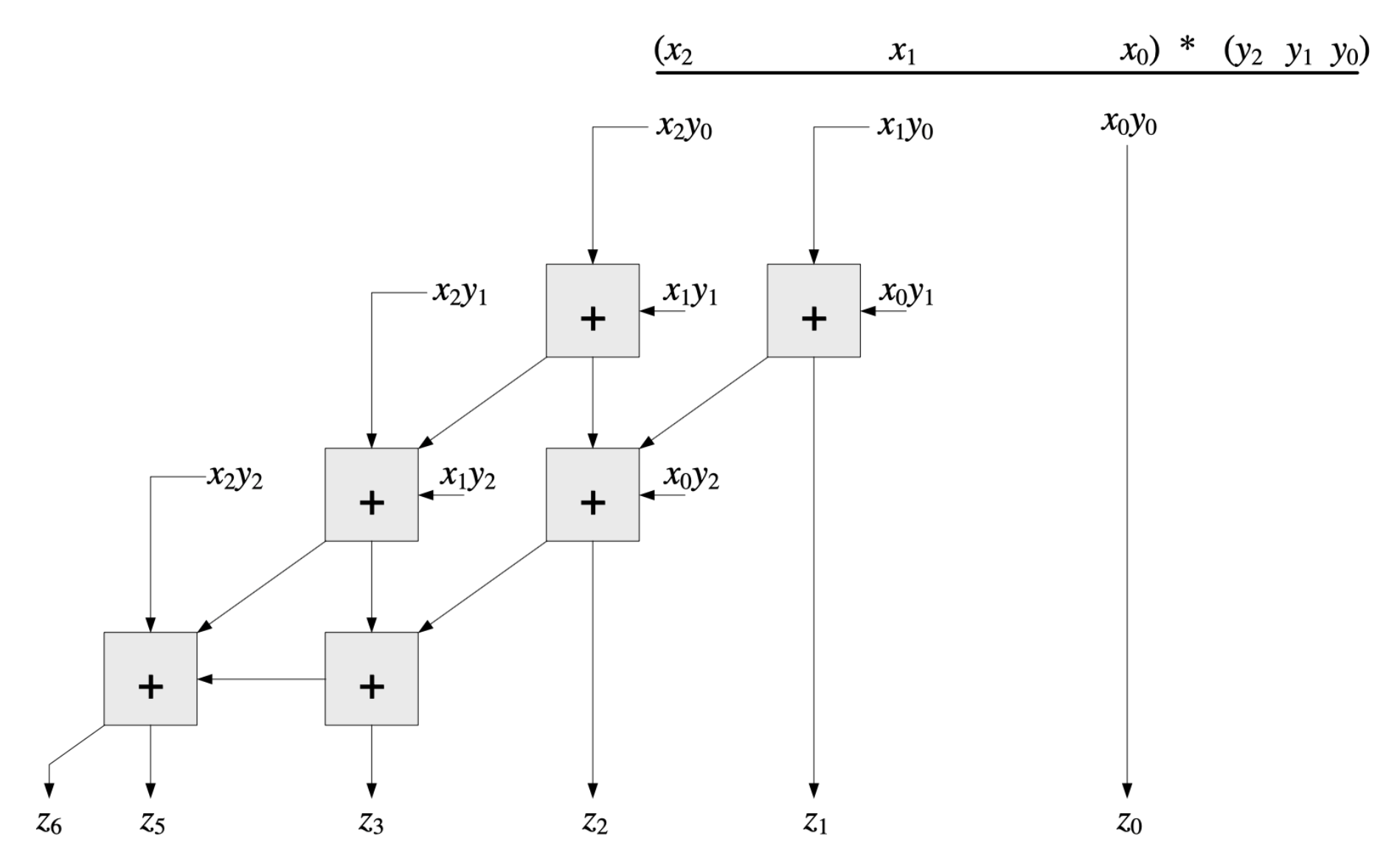
• Overhead
  • Hardware: $O(n^2)$ gates
    • $n^2$ 2-bit multiplications: $n^2$ 2-AND gates
    • $n$ n-bit additions: $n(n-1)$ full adders
  • Delay: $O(n)$

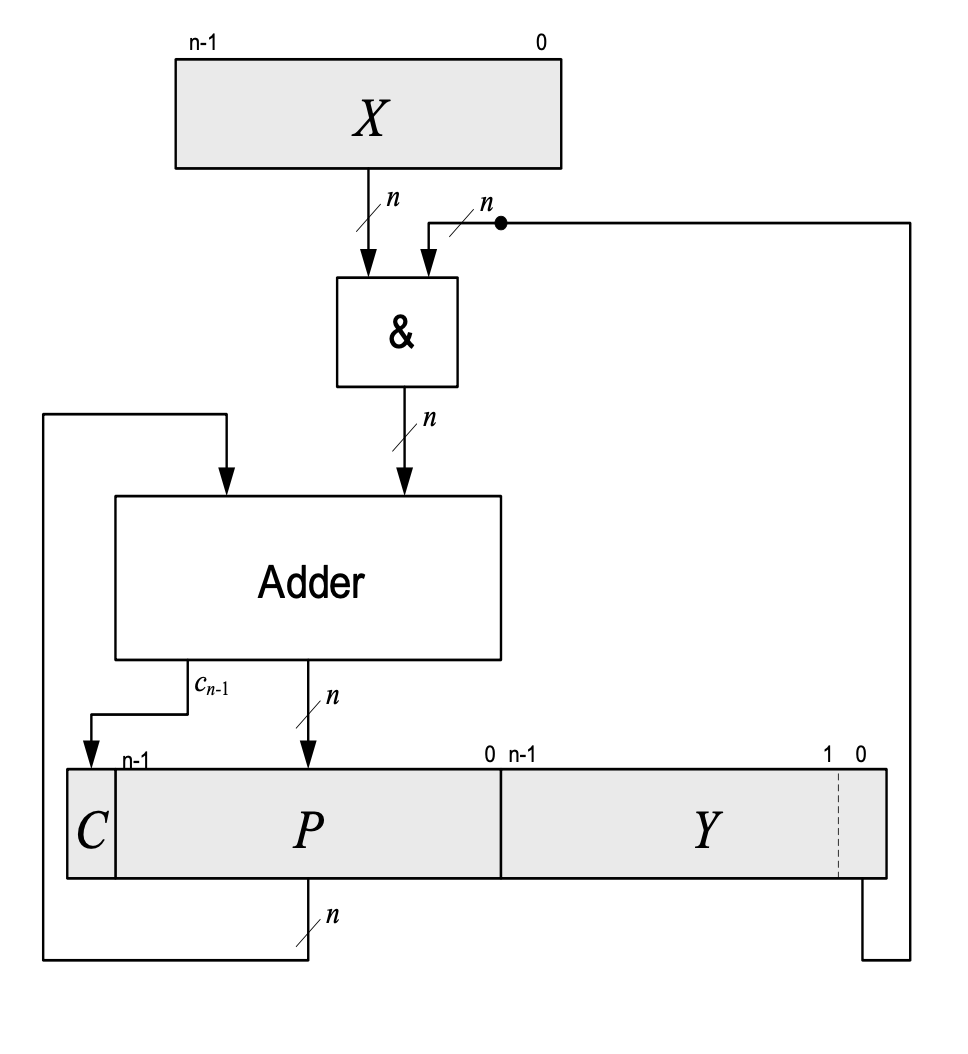
Sequential Multiplier

• Partial sums are accumulated stepwise
• Notes
  • Y is stored in a partial sum register → save 1 register
  • ‘logic shift’, i.e. fill right with 0s
• Algorithm
  1. Load X,Y
  2. C←0, P←0
  3. Iterate n-times:
     1. if Y(0)=1
        1. then P←P+X
        2. else P←P+0
     2. shift (C,P,Y) 1 digit left
  4. Result is in (P,Y)
• 

Signs

• Sign Magnitude
  1. Compute magnitude and sign $x=(s_x|x|),y=(s_y|y|)$
  2. Multiply the magnitudes
  3. Compute the sign of the result $s_z=s_x\oplus s_y$
  4. Negate the result if negative
• 2’s Complement
  • If $x<0$
    • ‘Arithmetic shift’ (signed shift, sign extension) : shift left with sign instead of 0
    • Sign in position $p_{n-1}$; on overflow in $c_{n-1}$ → shift $p_{n-1}+c_{n-1}$
  • If $y<0$
    • Then $(2^n-|y|)x$ is what was computed
    • We need to subtract $2^{n}x$ through $P\leftarrow P–x$ to get the correct result

Booth Multiplier

• Optimization
  • No need to add when $y_i=0$, only shift
  • It is not necessary to perform $(m+1)$ additions when there is a chain of $(m+1)$ 1‘s in y
    • We just need to subtract X at the begin of the chain and add X back at the end of the chain
    • $x{\sum }_{j=i}^{i+m}{2}^i=x\left({\sum }_{j=0}^{i+m}{2}^j-{\sum }_{l=0}^{i-1}{2}^l\right)=x(2^{i+m+l}-1-2^i+1)=x(2^{i+m+l}-2^i)$
      • Where $i$ is the first digit that is 1 and $m$ is the number of consecutive 1s (so $i+m$ is the last 1 in the chain)
• Booth Recoding: $y$ is translated to $y^{\prime }$
  1. $y$ is extended by $y_{-1}=0$
  2. $y^{\prime }$ is built as follows $y_i^{\prime }=y_{i-1}–y_i$
• Meaning of $y^{\prime }$:
  • $y^{\prime }=0$: shift right
  • $y^{\prime }=-1$ (represented “S”): P –= x then right shift (begin of a chain of 1s)
  • $y^{\prime }=1$ (represented “A”) : P += X then right shift (end of a chain of 1s)
• Requires an addition and subtraction for each chain
  • Weakness: when multiplier alternates between 0s and 1s
  • Can sometimes be avoided by switching the first and second operands