Inner Products

A function that assigns to every ordered pair of vectors $x,y\in V$, a scaler in $F$ denoted $⟨x,y⟩$ such that $\forall x,y\in V$ and $\forall c\in F$, the following hold

• $⟨x+z,y⟩=⟨x,y⟩+⟨z,y⟩$
• $⟨cx,y⟩=c⟨x,y⟩$
• $\overline{⟨cx,y⟩}=⟨y,x⟩$ (complex conjugation)
• $⟨x,x⟩>0$ if $x\ne 0$

An inner product space (ips) is a vector space with a specified inner product

Common Types

• Tuples: Dot Product
• Matrices: Frobenious inner product $⟨A,B⟩=\text{tr}(B^{\ast }A)$

Properties

• $⟨x,y+z⟩=⟨x,y⟩+⟨x,z⟩$
• $⟨x,cy⟩=\overline{c}⟨x,y⟩$
• $⟨x,0⟩=⟨0,x⟩=0$
• $⟨x,x⟩=0⟺x=0$
• $⟨x,y⟩=⟨x,z⟩,\forall x\in V⟹y=z$

Norm

• $\Vert x\Vert =\sqrt{⟨x,x⟩}$
• Properties
  • $\Vert cx\Vert =|c|\Vert x\Vert$
  • $\Vert x\Vert =0⟺x=0$
  • $\left|⟨x,y⟩\right|\le \Vert x\Vert \Vert y\Vert$ (Cauchy-Schwartz inequality)
  • $\Vert x+y\Vert \le \Vert x\Vert +\Vert y\Vert$ (triangle inequality)
• $x\in V$ is a unit vector if $\Vert x\Vert =1$

Orthogonal Sets

• $x,y\in V$ are orthogonal (perpendicular) if $⟨x,y⟩=0$
• $S\subseteq V$ orthogonal if any two two distinct vectors in $S$ are orthogonal
• $S\subseteq V$ orthonormal if $S$ is orthogonal and contains entirely unit vectors
• $S$ is an orthogonal subset of $V$ consisting of nonzero vectors $⟹S$ is linearly independent

Using

• $S=\{v_1,\dots ,v_k\}$ orthogonal subset of $V$, $v_i\ne 0$.
• $y\in \text{span}(s)⟹y=\sum _{i=1}^k\frac{⟨y,v_i⟩}{{\Vert v_i\Vert }^2}{v}_i$
• finding the projection of y onto each vector and then adding them together
• If orthonormal, can drop the division because it’s just dividing by 1

Gram-Schmidt Orthogonalization

$S=\{w_1,\dots ,w_n\}$ linearly independent subset of inner product space $V$ Define $S^{\prime }=\{v_1,\dots ,v_n\}$ where $v_1=w_1$ and

$$v_k=w_k-\sum _{j=1}^{k-1}\frac{⟨w_k,v_j⟩}{{\Vert v_j\Vert }^2}{v}_j,2\le k\le n$$

$⟹S^{\prime }$ is an orthogonal set of nonzero vectors and $\text{span}(S^{\prime })=\text{span}(S)$

Works by subtracting the projection of the current vectors onto all of the previous vectors from the current vector

Orthonormal Bases

• An orthonormal basis is an ordered basis that is orthonormal
• Bases are nicer to work with when orthonormal (because you can reason about them more like the standard coordinate system)
• $V$ nonzero finite-dimensional ips. Then $V$ has an orthonormal basis $\beta$
• Using as linear combination
  • $\beta =\{v_1,\dots ,v_n\}$ and $x\in V$
  • $x=\sum _{i=1}^n⟨x,v_i⟩v_i$
  • Corollary for Matrix Representations of Transforms
    • Let $T$ be linear operator on $V$ and $A=[T{]}_{\beta }$. Then $\forall i,j,A_{ij}=⟨T(v_j),v_i⟩$

Orthogonal Complement

• $S\subset V$ ips. $S^{\perp }=\{x\in V:⟨x,y⟩=0\forall y\in S\}$ is the orthogonal complement of $S$.
• It is the set of vectors in $V$ that are orthogonal to every vector in $S$
• $S^{\perp }$ is a subspace of $V$

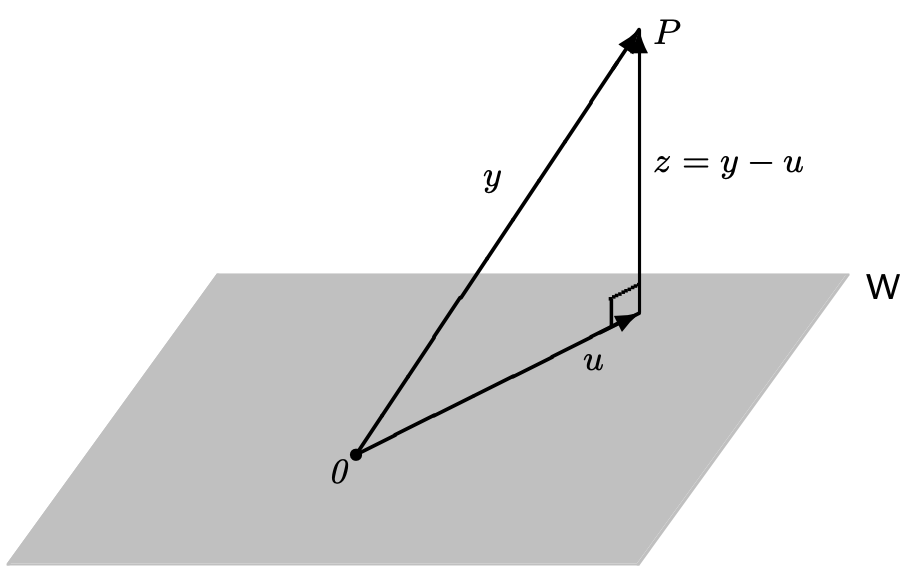
$W$ finite-dimensional subspace of ips $V$. Let $y\in V$. Then $\exists !u\in W,z\in W^{\perp }$ such that $y=u+z$ Furthermore, if $\{u_1,\dots ,u_k\}$ is an orthonormal basis for $W$ $⟹u=\sum _{i=1}^k⟨y,v_i⟩v_i$ the $u$ here is the “closest” to $y$. that is for any $x\in W,\Vert y-x\Vert \ge \Vert y-u\Vert$. That is an equality iff $x=u$.

3 dimensional example:

$S=\{v_1,\dots ,v_k\}$ is an orthonormal subset of ips $V$

• $S$ can be extended to an orthonormal basis $\{v_1,\dots ,v_k,v_{k+1}\dots ,v_n\}$ for $V$
• If $W=\text{span}(S)$ then the vectors that were added above is an orthonormal basis for $W^{\perp }$
• If $W$ is any subspace of $V$, then $\dim (V)=\dim (W)+\dim (W^{\perp })$