Lines

Definitions

Unique Attributes of Every Line

• $P_0\in \mathcal{L}$
• $\vec{v}\parallel \mathcal{L}$

Geometric

$$\mathcal{L}=\{P\mid \overrightarrow{P_{0}P}\parallel \vec{v}\}$$

Algebraic

• A line is uniquely defined as

  • $P_0\in \mathcal{L}$
  • $\vec{v}\parallel \mathcal{L}$

• Vector:

  • for every input value $t$, $\vec{r}$ is the position vector for a point on the line
  • $\vec{r}(t)=\overrightarrow{O{P}_0}+t\vec{v}=⟨x_0,y_0,z_0⟩+t⟨v_1,v_2,v_3⟩$

• Parametric:

  • A rearranged vector form

$$\begin{array}{r}x=x_0+t{v}_1\\ y=y_0+t{v}_2\\ z=z_0+t{v}_3\end{array}$$

• Symmetric
  • $\frac{x-x_0}{v_1}=\frac{y-y_0}{v_2}=\frac{z-z_0}{v_3}$
  • If $v_1$, $v_2$, or $v_3$ are $0$, that part is removed from the main equality and written separately as the variable being equal to the respective given point component
  • Geometric significance: means a line can be represented as the intersection between two planes (because the double equality can be split up into the form $x=y$ and $y=z$)

Mutual Orientation

Using Points

(A & B on line one. C & D on line 2)

• Parallel $⟺\overrightarrow{AB}\times \overrightarrow{CD}=0$ (also $\overrightarrow{AB}=s\overrightarrow{CD}$)
• Intersecting $⟺\overrightarrow{AD}\cdot \left(\overrightarrow{AB}\times \overrightarrow{CD}\right)=0$
• Skewed $⟺\overrightarrow{AD}\cdot \left(\overrightarrow{AB}\times \overrightarrow{CD}\right)\ne 0$

Using Line Equation

• Parallel $⟺\overrightarrow{v_1}\times \overrightarrow{v_2}=0$ (also $\overrightarrow{v_1}=s\overrightarrow{v_2}$)
• Intersecting $⟺\overrightarrow{P_1{P}_2}\cdot \left(\overrightarrow{v_1}\times \overrightarrow{v_2}\right)=0$
• Skewed $⟺\overrightarrow{P_1{P}_2}\cdot \left(\overrightarrow{v_1}\times \overrightarrow{v_2}\right)\ne 0$

Intersections With

Another Line

$\overrightarrow{r_1}(t)=\overrightarrow{r_2}(s)$

• Infinite solutions → same line
• One solution → $\overrightarrow{O{P}_0}=\overrightarrow{r_1}(t)=\overrightarrow{r_2}(s)$
• No solutions → No intersection (skew or parallel)

A Plane

• $\vec{v}$ intersects the plane at $P_0$ and $P_2$ is another point on the line
• $P_1$ is another point on the plane
• $\vec{n}$ is the normal vector of the plane

$$t=\frac{\vec{n}\cdot \overrightarrow{P_2{P}_1}}{\vec{v}\cdot \vec{n}}$$

If $\vec{v}\cdot \vec{n}=0$ then the line lies in the plane

Any Shape

1. Get parametric equation for line
2. Plug parametric equation into $x,y,z$ of the shape’s equation
3. Solve for $t$
4. Plug found $t$ value into parametric equation to get coordinates for the point(s) of intersection

Finding

Distance Between Skewed Lines

We are trying to find the distance between sets

We can create a parallelepiped with vectors created from the two lines

$$D=h=\frac{V}{A}=\frac{\left|\overrightarrow{CA}\cdot \left(\overrightarrow{CD}\times \overrightarrow{AB}\right)\right|}{\Vert \overrightarrow{CD}\times \overrightarrow{AB}\Vert }$$ $$D=\frac{\left|\overrightarrow{P_1{P}_2}\cdot \left(\overrightarrow{v_1}\times \overrightarrow{v_2}\right)\right|}{\Vert \overrightarrow{v_1}\times \overrightarrow{v_2}\Vert }$$

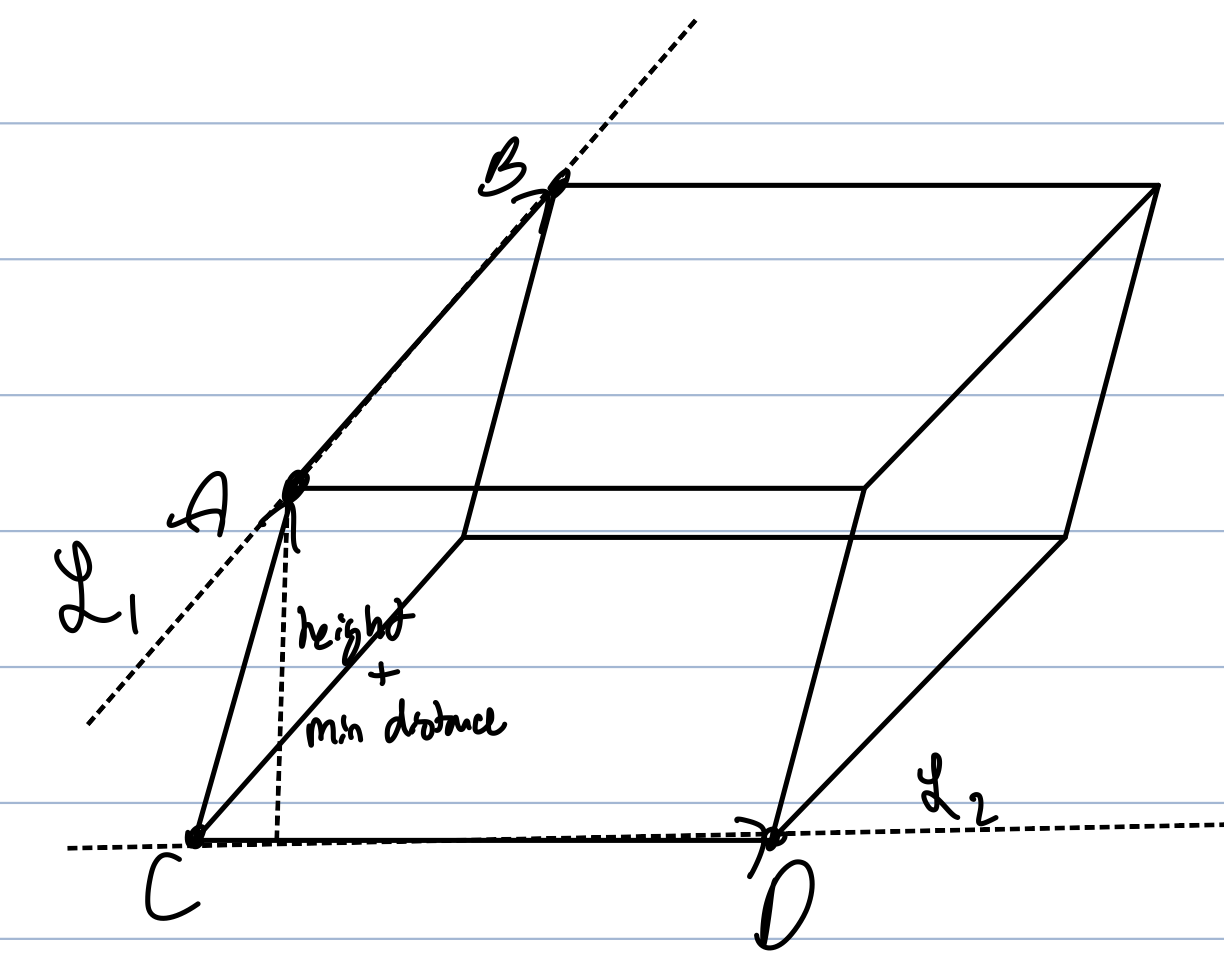
If Line on Plane

• Find $P_0$ by finding a point that would satisfy the equations of both lines
  • Setting variables to 0 is your friend in this
• $\vec{v}=\overrightarrow{n_1}\times \overrightarrow{n_2}$

Distance From Line to a Point

$$D=\frac{\Vert \vec{v}\times \overrightarrow{P_0{P}_1}\Vert }{\Vert \vec{v}\Vert }$$

• Finds the volume of the parallelogram formed by the vector and the vector to the point and then divides by width to get height